背景简介

材料力学性能评估对设备设计和运行至关重要，尤其金属材料的拉伸、蠕变和疲劳性能，通常通过单轴试验评估，每种力学性能的具体测试方法在ASTM均有相应的标准。单轴试验可直接获取应力应变数据，但存在材料消耗大、评估周期长的问题，难以用于稀缺新材料、核电站监督试样及增材制造金属的局部性能评估。因此，小冲杆试验（Small Punch Test, SPT）应运而生，其试样体积仅为单轴试验的1/200，能节省材料和时间，还可反映局部性能。但SPT需将载荷-位移数据转换为应力-应变数据，且因加载机制（多轴、间接加载）与单轴试验不同，转换难度大。目前SPT仅限拉伸和蠕变评估，虽有研究尝试拓展至疲劳领域，但数据转换效果不佳。本文旨在通过有限元法和等效方程，将SPT拓展到疲劳性能评估并验证。

（1）基于Chakrabarty膜拉伸理论和Mao的经验方程，建立等效应力转换方程。等效应力的计算公式如下：

冲头位移ν与试样和冲头之间的接触角φ，可通过如下方程表示：

上述方程的逆形式可通过如下方程非线性拟合获得：

根据Mao通过试验结果总结的经验方程可得如下方程：

联立上述方程可获得等效应力转换方程，如下所示：

其中，σ_eq为等效应力，F为载荷，h为变形试样的最小厚度，R为冲头半径，φ为试样与冲头之间的接触角。此外，还需要考虑试样与冲头之间的摩擦对模拟结果的影响。通过引入无量纲校正因子α_σ,h，反应试样最小厚度随摩擦系数的变化，公式如下：

如图1所示，SPT载荷转换为单轴应力时由于摩擦引起的应力退化可通过无量纲校正因子α_σ,A表示：

因此，考虑摩擦因素后的等效应力转换方程的完整形式表示如下：

其中，σ'_eq表示修正的等效应力。修改后的等效方程更准确地考虑了接触和材料组合产生的摩擦，与现有方程相比，提供了更好的转换性能。

图1 半球形冲球（A_halfsphere）和接触面积（A_μ）示意图

（2）构建了小冲杆疲劳试验的有限元分析模型。通过上下冲头的基准点模拟了小冲杆疲劳试验的循环加载。负载比R = F_min/F_max = -1，三角波形中的频率为1 Hz，使用每个周期由四个等距级组成的加载机制实现，如图2所示。试样与冲头之间的摩擦对疲劳损伤有显著影响。如图3所示，通过有限元分析评估了改性9Cr-1Mo钢试样在550℃下的垂直载荷与摩擦系数之间的四种相关性，公式如下：

在进行小冲杆疲劳试验有限元分析时，必须定义试样和冲球之间摩擦系数的特定值。小冲杆疲劳试验的摩擦系数最终确定如下：

通过上述分析建立了小冲杆疲劳试验的有限元分析模型。

图2 循环加载条件的示意图

图3 小冲杆疲劳试验中冲头球与试样之间的摩擦系数

（3）小冲杆疲劳试验模拟结果分析：基于修正的 Wahab 疲劳损伤模型，在四种不同最大载荷（570.9N、610.3N、648.5N、685.9N）下进行小冲杆疲劳试验有限元分析，观察到疲劳损伤演变规律：试样上下表面附近单元先达到最大损伤变量，随加载循环进行，损伤从表面向中心扩展，最终上下表面损伤单元在中心汇合时材料失效，如图4所示。

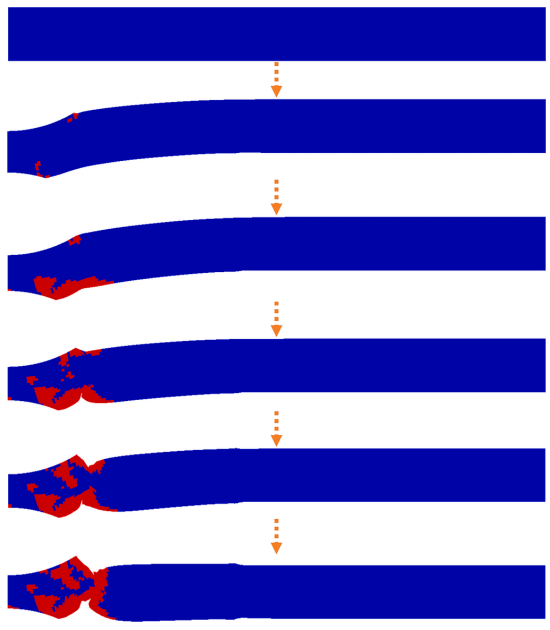
图4 有限元方法小冲头疲劳试验中的疲劳损伤演化

（4）基于小冲杆疲劳试验的S-N曲线。分别采用现有等效方程和修正等效方程，将小冲杆疲劳试验的最大载荷转换为对应应力，如图5所示。与单轴疲劳试验结果对比，基于现有等效方程的小冲杆疲劳试验S-N曲线与单轴疲劳试验曲线偏差较大，而基于修正等效方程的曲线与单轴疲劳试验曲线高度相似，因修正方程通过无量纲修正因子更准确反映摩擦影响，验证了小冲杆疲劳试验用于疲劳损伤评估的可行性，如图6所示。

图5 改性9Cr-1Mo钢在550°C下小冲杆载荷与等效单轴应力之间的相关性

图6 基于小冲杆和单轴疲劳试验的S-N曲线比较

致谢

这项工作得到了韩国教育部资助的韩国国家研究基金会（NRF）的支持[资助号：2021R1A6A1A03039696];由科学和信息通信技术部资助的韩国国家研究基金会 （NRF） [资助号：2022R1F1A1071390];由韩国政府 （MSIT） 资助的韩国国家研究基金会 （NRF） [资助号：2022R1C1C1007659]。本文第一作者和通讯作者：Sangyeop Kim（Sungkyunkwan University）。

本期小编 郭子键（整理）

董乃健（校对）

  程　航  （审核）

董乃健（发布）