背景简介

水凝胶因其与生物组织相似的柔软度和生物相容性，在生物医学和软驱动器领域应用广泛。其机械性能对溶剂含量极为敏感。传统观点认为充分溶胀的水凝胶为超弹性材料。然而，在干燥或脱溶胀状态下，水凝胶表现出显著的粘弹性和不可逆形变（Inelastic deformation）。这种不可逆响应被推测是由于溶剂减少导致分子间链距离缩短，从而增强了氢键或范德华力等分子间相互作用所致。尽管水凝胶具有优异的特性，但在实际应用中，尤其是在生物医学（如植入物）或软驱动器等对材料稳定性要求较高的领域，准确预测其随溶剂含量变化的长期机械性能是一个重大挑战。现有的力学模型多基于超弹性理论，往往忽略了溶剂含量变化导致的粘弹性效应。对于干燥或半干燥状态下水凝胶的时间依赖性行为和不可逆形变，缺乏统一且定量的理论框架进行准确描述和预测。特别是，如何将微观的分子间相互作用机制与宏观的本构关系进行有效且简化的桥接，仍是软物质力学领域的一个悬而未决的问题。因此，迫切需要开发一种能够全面考虑水凝胶动力学、微观分子间相互作用，并能在工程尺度上实现定量预测的粘超弹性模型，以指导水凝胶材料的可靠设计和应用。

成果介绍

（1）该研究首先制备了不同溶剂含量（充分溶胀、原样以及干燥至60wt%和80wt%）的聚丙烯酰胺（PAG）水凝胶试样，以系统地考察不同分子间距离对机械性能的影响。为确保单轴拉伸-卸载试验数据的精确性，实验采用了先进的数字图像相关（DIC）方法对试样表面的应变场进行实时测量（图1, 图2），有效地排除了夹具滑移等潜在的误差。核心实验结果（图3）清晰地表明，水凝胶的应力水平随着溶剂含量的减少而显著增加。更关键的是，干燥水凝胶（如 60wt%和80wt%）在加载-卸载循环中表现出巨大的滞后环，即明显的不可逆形变和卸载后的残余应变；相比之下，充分溶胀（SW）水凝胶的滞后环极小，行为接近纯超弹性。这一关键发现从宏观力学角度直接证实了：当溶剂减少导致分子间链距离缩短时，分子间相互作用的增强是水凝胶产生显著粘弹性和不可逆形变的根本物理机制。

图1 测试过程中水凝胶试样的连续数字图像。使用水彩墨水笔在水凝胶试样表面绘制点阵图案。在各点周围生成位移测量点，并利用这些测量点构建三角单元网格以评估应变场的发展

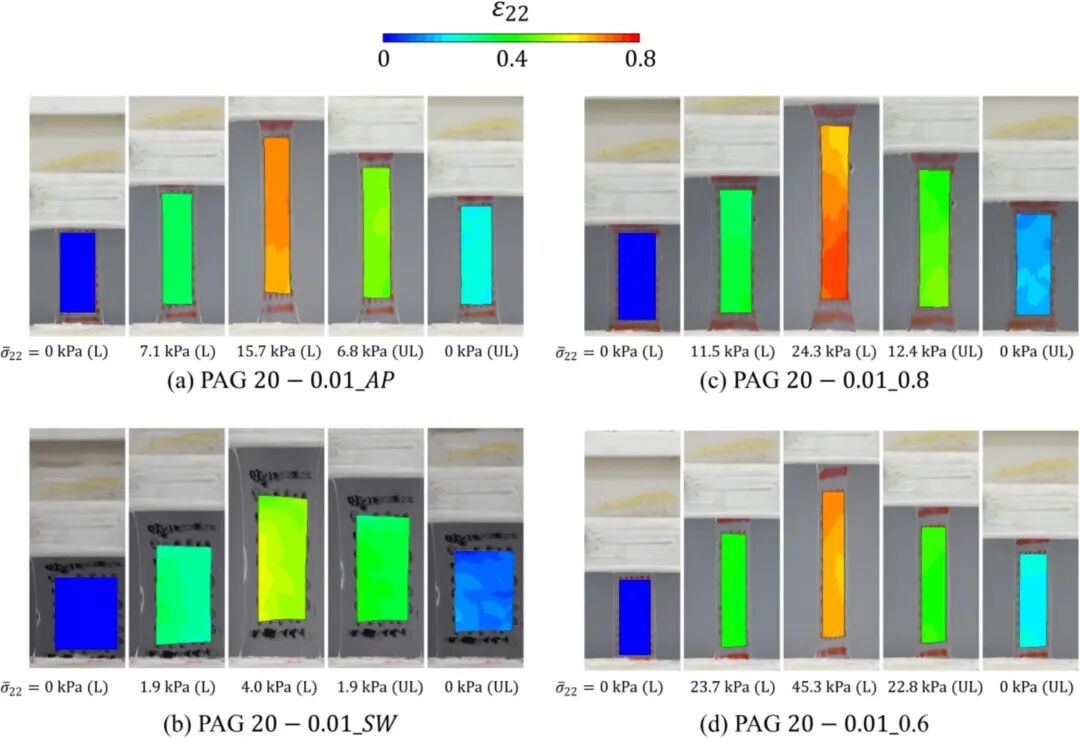
图2 在单轴拉伸加载-卸载试验中应变的发展情况：（a）PAG 20 − 0.01_AP，（b）SW，（c）0.8，（d）0.6。图中数值代表施加应力，(L)和(UL)分别表示“加载”和“卸载”

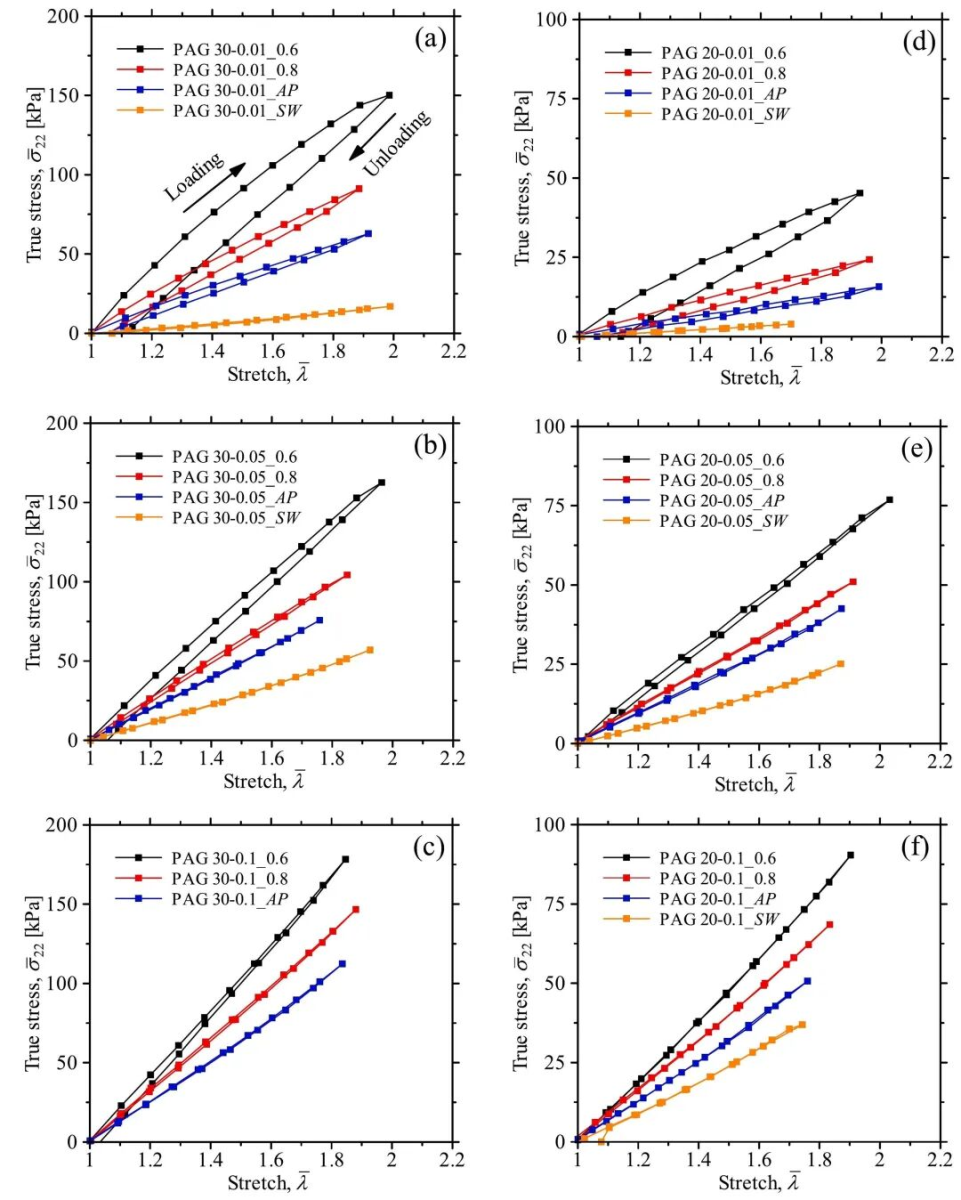
图3 真应力与真应变的关系曲线：(a) PAG 30 − 0.01，(b) 0.05，(c) 0.1，(d) 20 − 0.01，(e) 20 − 0.05，(f) 20 − 0.1。黑色、红色、蓝色和橙色曲线分别代表C^x – C^y_0.6、0.8、AP和SW的模型。需注意(a)-(c)与(d)-(f)图中纵坐标刻度不同

（2）基于实验对分子间相互作用的定量评估，研究建立了基于瞬态网络（TN）理论的粘超弹性模型来描述水凝胶在不同状态下的复杂行为。该模型采用一个并联机械系统（图4）来解耦力学响应：一个交联（CL）网络负责可逆的超弹性响应，而一个次级键（SB）网络则专门负责由分子间相互作用引起的不可逆粘弹性响应。为了在模型中反映溶剂含量对机械性能的影响，研究创新性地引入了无量纲参数ϕ来表征水凝胶的分子间链距离（图5）。通过将次级键（SB）链的密度n^SB与该参数ϕ关联起来（n^SB∝(1-ϕ)³），模型实现了对分子间相互作用引起的粘弹性贡献大小的定量调节，即溶剂含量越低，ϕ越小，SB链密度越大，粘弹性贡献越强。最终，该模型的数值模拟结果（图6）与不同溶剂含量和不同初始组分下水凝胶在加载-卸载循环中的应力-应变滞后行为高度吻合，证明了该模型在预测水凝胶粘超弹性行为方面的准确性和普适性。

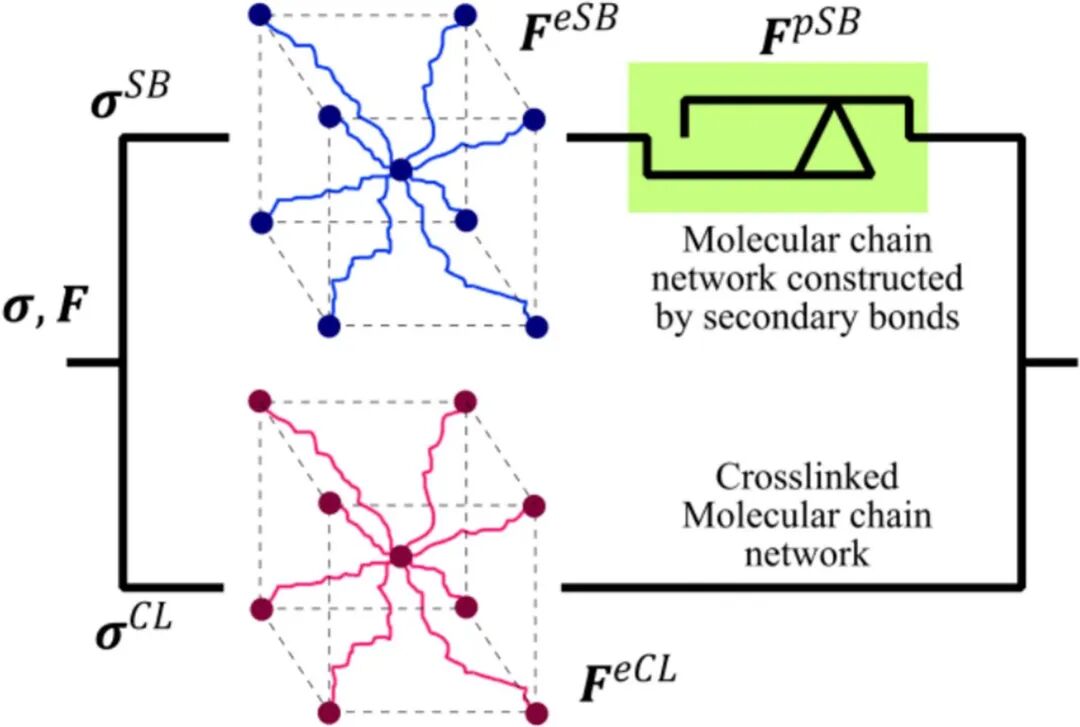
图4 由CL和SB分子链网络构成的平行机械系统。熵弹性弹簧配置于CL线，而熵弹性弹簧与非弹性滑块则配置于SB线

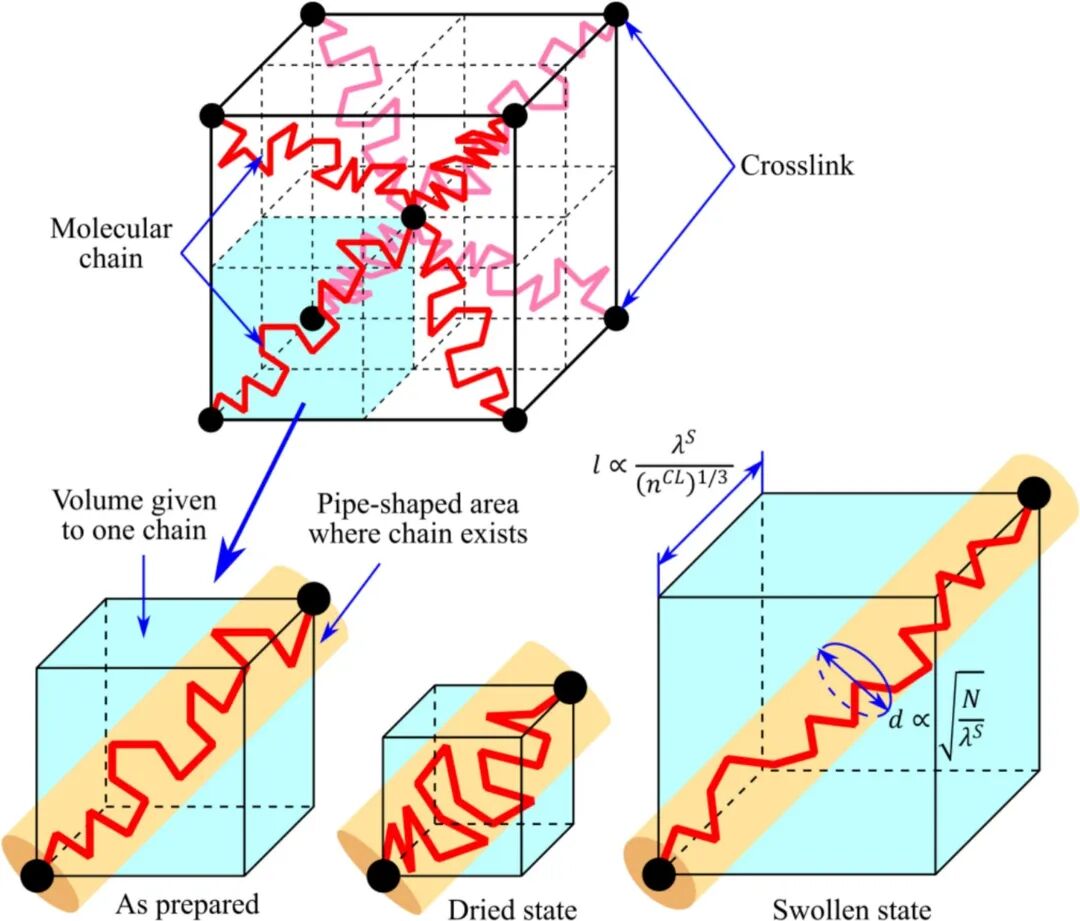
图5 膨胀与干燥过程中分子间链距变化示意图。单条链所占体积由浅蓝色立方体表示，而链体所在的管状区域则由浅棕色管道描绘

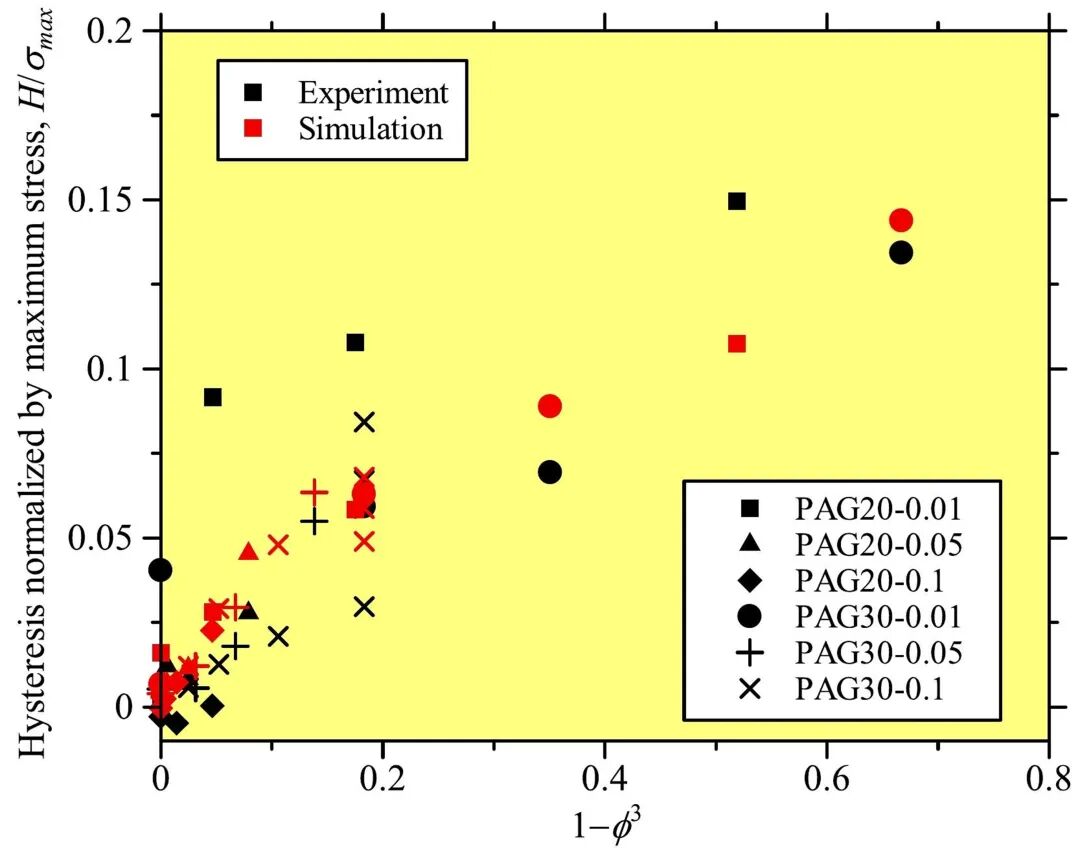
图6 滞后损耗与(1 − ϕ)³的关系。ϕ是通过式(7)获得的无量纲参数，代表分子间链距。利用该参数可计算出不同单体与交联剂密度及溶剂含量的所有水凝胶试样的滞后损耗

致谢

本文第一作者和通讯作者：Makoto Uchida（Osaka Metropolitan University）。

本期小编 沈文顺（整理）

吴林森（校对）

郭子键（审核）

董乃健（发布）