|
Long D J, Dunne F P E. On the Mechanistic Driving Force for Short Fatigue Crack Path[J]. Journal of the Mechanics and Physics of Solids, 2023: 105368.
Long, Daniel J., and Fionn PE Dunne. "On the Mechanistic Driving Force for Short Fatigue Crack Path." Journal of the Mechanics and Physics of Solids (2023): 105368.
Long, D. J., & Dunne, F. P. (2023). On the Mechanistic Driving Force for Short Fatigue Crack Path. Journal of the Mechanics and Physics of Solids, 105368.
背景简介
在多晶微结构中,短裂纹路径会显著影响裂纹扩展速率,通常可以使用数值模拟方法来预测短裂纹扩展。在晶体塑性有限元(Crystal plasticity finite element,CPFE)模型中,最常用于预测短裂纹扩展路径的准则是最大滑移准则,该准则在多晶材料中表现出很强的微观结构敏感性。然而由于局部应力状态不会根据裂纹尖端位置进行更新,因此这种方法未捕获裂纹路径的晶粒内部变化。同时文献中大量实验证据证明,最大滑移量可能不是疲劳短裂纹扩展路径的唯一决定因素。因此,有必要探索新的和替代的预测方法。
在本研究中,假设短裂纹路径部分由晶体学滑移控制(裂纹成核由滑移活动主导是没有争议的)。将CPFE模拟的微观结构路径与扩展有限元法(Extended finite element method,XFEM)相结合,通过(i)最大滑移准则、(ii)最大能量释放率和(iii)最大法向储能密度准则直接与实验结构进行比较,验证了这一假设。
成果介绍
本文基于位错滑移活动在控制短疲劳裂纹路径中起关键作用但不是主导因素的假设,提出了两种基于能量的新准则。本文采用这两种新的准则和传统的最大滑移准则,并与多晶Zircaloy-4合金的实验结果进行比较。总体而言,提出的最大法向储能密度准则被证明是预测真实微观结构中裂纹路径的最可靠和最鲁棒的方法,它能够捕获HCP单晶中的裂纹路径曲折现象。最大能量释放率准则预测也显示出与实验裂纹路径的良好吻合性,但可能需要裂纹分岔能力才能充分发挥其潜力。本文得出以下结论:
(1)每种裂纹路径选择方法均采用微观结构敏感的储能密度(Stored energy density,SED)作为断裂准则(仅用于扩展)。SED是位错结构在塑性变形过程中积累的可恢复能量的度量,其在CPFE模型中的表达如下式所示。
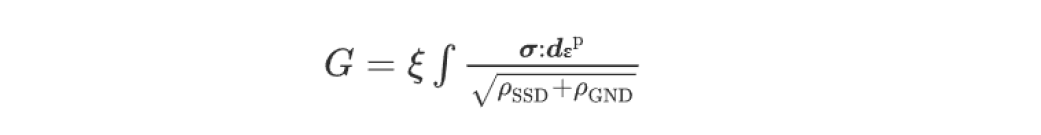
(其中σ为应力张量,dεp为塑性应变增量,ρSSD和ρGND分别为统计存储位错(SSD)密度和几何必要位错(GND)密度,ξ为以位错结构弹性存储的塑性应变能的可恢复部分所占百分比,这里假设等于5%。)
(i)最大滑移准则:
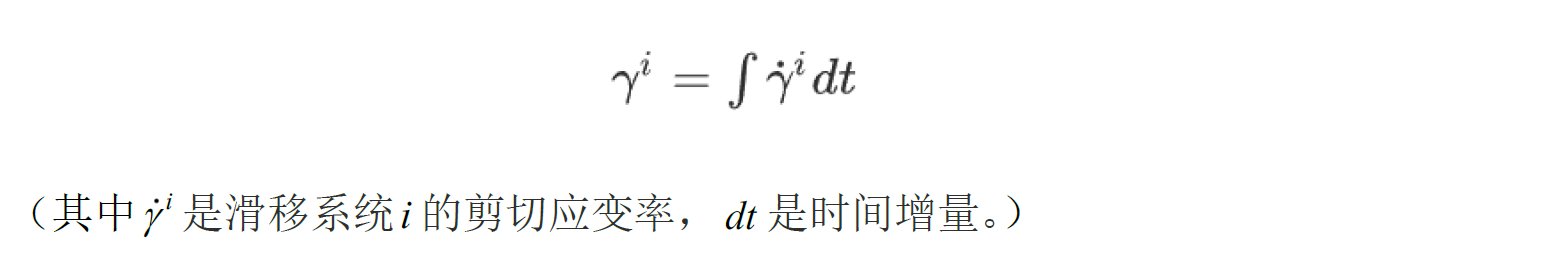
(ii)最大能量释放率准则:
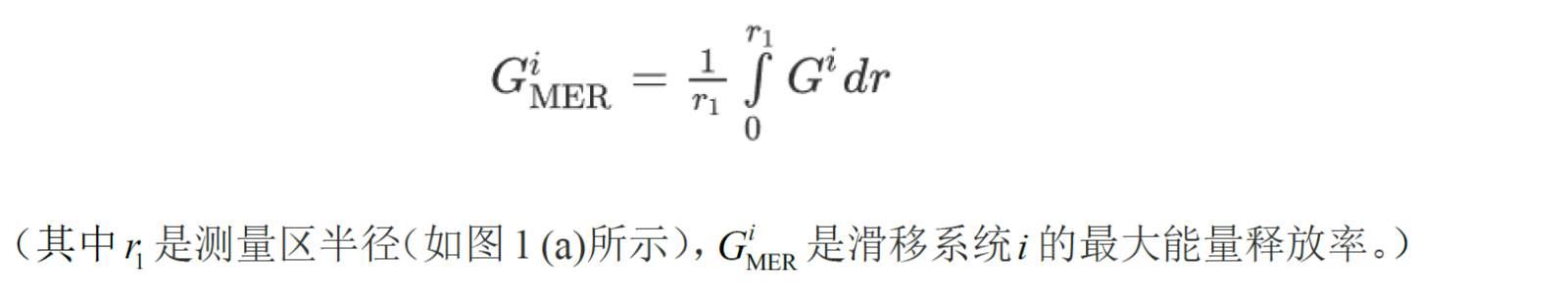
(iii)最大法向储能密度准则:
.png)
.jpg)
图1 (a) 利用有限元网格实现最大能量释放率准则的示意图。其中测量区是指以裂纹尖端为中心的半圆形区域;测量子区域是跨越单个滑动轨迹的圆形区域,包含有限元网格中的积分点。(b) 描述裂纹路径法向储能密度准则的示意图。其中红色和蓝色箭头分别表示应力和塑性应变张量的分量,它们分别垂直于裂纹面。法向分量的计算是考虑三维裂纹平面的方向,由它们的单位法向量ni给出
(2)本文利用电子背散射衍射(EBSD)对裂纹附近的微观结构和晶体形貌进行表征,建立的有限元模型如图2所示。单晶模拟结果如图3所示,最大法向储能密度准则准确的预测了第一个方向的曲折裂纹路径(图3 (i- j)),这与最大滑移率结果(图3 (a- d))略有不同。对于第二个方向,三种方法中均产生了相同的结果,即沿棱柱形滑动平面的直线裂纹路径。由于第三个(垂直)棱柱滑移系统几乎不活动,因此无法使用任何方法预测其裂纹扩展路径。
.jpg)
图2 CPFE模型结构。其中自由表面EBSD数据用于重建二维微观结构;建立了厚度仅为150μm的三维模型,以准确表征自由表面应力状态;垂直边界条件用于表示三点弯曲结构中的支撑销,在试样顶部表面的一个区域施加分布式循环载荷。
.jpg)
图3 三种准则预测单晶裂纹路径的比较:(a- d) 最大滑移率;(e- h) 最大能量释放率;(i- l) 最大法向储能密度准则。
(3)以两个Zircaloy-4试样(A和B)的疲劳裂纹扩展实验为例进行研究,并将短裂纹路径的三个准则预测的结果与两组实验数据直接进行比较,如图4所示。图4 (a)显示了最大滑移准则与实验结果之间的一致性,模拟路径最初由于沿棱柱平面的裂纹增长而向左偏离,而在此点之后呈现出相同裂纹路径的趋势。图4 (b)和(c)显示了使用最大能量释放率准则和最大法向储能密度准则的模型与实验之间的一致性。图5 (a)显示了最大滑移准则的模拟结果,对比试样B的实验路径,最大滑移准则的模拟路径明显偏离。
.jpg)
图4 三种短裂纹预测方法与A试样实验裂纹路径的比较。其中实验裂纹表面用红色阴影表示,模型预测裂纹表面用黑色阴影表示。(a) 采用最大滑移准则模拟裂纹路径;(b) 利用最大能量释放率准则模拟裂纹路径。由于局部收敛问题,模拟提前终止;(c) 采用最大法向储能密度准则模拟裂纹路径
.jpg)
图5 三种短裂纹预测方法与B试样实验裂纹路径的比较。其中实验裂纹表面用红色阴影表示,模型预测裂纹表面用青色阴影表示。(a) 采用最大滑移准则模拟裂纹路径;(b) 利用最大能量释放率准则模拟裂纹路径;(c) 采用最大法向储能密度准则模拟裂纹路径,并用扫描电镜图像详细显示了晶界附近实验裂纹路径的偏转
(4)最大能量释放率准则的预测也显示出与实验裂纹路径的良好一致性,但可能需要裂纹分岔能力才能完全发挥潜力,如图6所示。图6 (b)中预测的裂纹路径与实验一致,同时由于裂纹前储存的能量耗尽(即最大释放速率),裂纹沿替代棱柱平面向左扩展,如图6 (c)所示。当裂纹穿过晶界时,裂纹继续向下扩展直至最终停止扩展。
.jpg)
图6 基于最大能量释放率准则的裂纹扩展4个关键阶段的微观结构中的SED场。(a) 裂纹扩展前第15次疲劳循环(N = 15)时的SED场。其中测量半圆显示在手动插入的边缘裂纹前面,最大能量释放方向与实验结果一致;(b) 裂纹尖端的能量场。其中在半圆测量区内,存在一个原始裂纹扩展方向上能量耗尽的区域;(c) N = 135处的能量场,此时裂纹首先与晶界相互作用。由于实验裂纹扩展方向存在能量的再积累,裂纹明显远离最高SED区域扩展;(d) 最终裂纹扩展路径,由于晶粒间测量区的交叉,裂纹沿自终止方向扩展
本文通讯作者:Daniel J. Long(Department of Materials, Royal School of Mines, Imperial College London, SW7 2AZ United Kingdom)。
本期小编:邱 瑞(整理)
王永杰(校对)
程 航(审核)
闵 琳(发布)
|