|
引文格式:
Kim S, Ro U, Kim Y H, et al. Evaluation of creep properties using small punch creep test for modified 9Cr-1Mo steel[J]. Journal of Mechanical Science and Technology, 2022, 36(9): 4549-4561.
Kim, Sangyeop, et al. "Evaluation of creep properties using small punch creep test for modified 9Cr-1Mo steel." Journal of Mechanical Science and Technology 36.9 (2022): 4549-4561.
Kim, S., Ro, U., Kim, Y. H., Lee, T., & Kim, M. K. (2022). Evaluation of creep properties using small punch creep test for modified 9Cr-1Mo steel. Journal of Mechanical Science and Technology, 36(9), 4549-4561.
背景简介
超高温反应堆(VHTR)的压力容器由于在较高温度下长期运行,会发生蠕变损伤,对构件安全运行产生致命的不利影响。9Cr-1Mo钢被认为是VHTR压力容器的合适候选材料。为了克服传统单轴拉伸蠕变试验(UCT)的缺陷,尤其在不破坏在役设备结构完整性的角度,采用小冲杆蠕变试验(SPCT) 进行结构完整性评估,因此必须建立UCT的应变和应力与SPCT的位移和载荷之间的关系。
目前,已有一些学者将SPCT载荷和位移转化为UCT应力和应变数据,如何基于这些转换后的数据,并遵循Norton、Larson-Miller和Monkman-Grant的三角关系,构建在一定温度下仅使用SPCT对改性9Cr-1Mo钢进行蠕变性能评估的模型,对评估9Cr-1Mo蠕变性能参数具有重要的意义。
成果介绍
(1)在550℃的高温下,在四种不同的载荷条件下对改性9Cr-1Mo钢进行SPCT:62.5 kgf、65 kgf、70 kgf 和75 kgf。图1显示了冲头位移随时间的曲线,与UCT应变随时间的变化曲线相似。
.png)
图1 550°C下改性9Cr-1Mo钢的小冲头蠕变试验曲线:(a)62.5 kgf;(b)65kgf;(c)70kgf;(d)75kgf
(2)基于Chakrabarty的膜拉伸理论,将SPCT的位移转换为UCT的应变,等效应变εeq可以用以下形式表示,其中h是冲头的位移:
.jpg)
基于Chakrabarty的膜拉伸理论,将SPCT的载荷转换为UCT的应力,并且考虑了冲头和试样的接触角以及摩擦影响,等效应力σeq可以用以下形式表示:
.jpg)
与UCT的应变曲线一样,等效应变曲线由四个阶段组成:瞬时变形、一次蠕变、二次蠕变和三次蠕变阶段。Norton和Monkman-Grant模型使用最小应变率而非应变来评估金属材料的蠕变特性,因此需要从等效应变曲线中选择最小应变率的额外过程。第二蠕变阶段的蠕变应变速率最小且恒定,因此选择基于蠕变寿命的30%-70%范围内的等效应变率平均值作为代表性最小等效应变率。
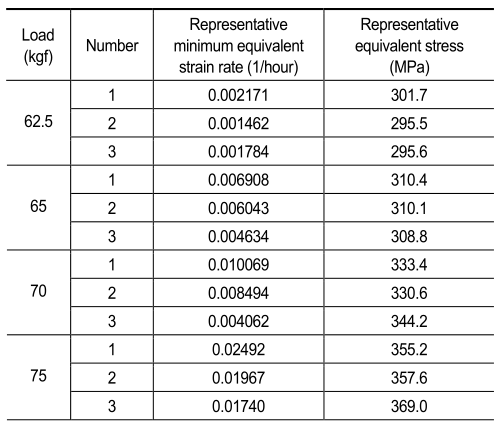
UCT在施加应力的整个时间内具有恒定的应力值,因为试样处于单轴应力状态。然而,与UCT不同,SPCT等效应力值在应力施加开始时迅速减小,在试样断裂前迅速增大,这是因为试样处于多轴应力状态。由于Norton和Larson- Miller模型使用应力来评估金属材料的蠕变特性,因此同样必须在变化的等效应力值中选择30%-70%范围内的等效应力平均值作为代表值,如图2所示。表1给出了仅通过SPCT得出的各荷载条件下的代表性等效最小应变率和代表性等效应力值。
.png)
图2 550℃下改性9Cr-1Mo钢的等效应变、应变率和应力曲线:(a)62.5 kgf;(b)65 kgf;(c)70 kgf;(d)75 kgf
表1 550℃下改性9Cr-1Mo钢的等效应变和应力分析结果
(3)通过SPCT数据构建的三个蠕变性能评估模型之间建立三角关系。Norton和Larson-Miller模型将应力作为共同变量,Larson-Miller和Monkman-Grant模型包含蠕变寿命,Monkman Grant和Norton模型包含最小应变率。通过与这些二元集合中的公共变量之间的三角关系,重新定义两个模型的每个集合的公共变量来构建最终模型,如图3所示。通过SPCT和三角关系构建的蠕变性能评估模型显示出非常相似的结果。
.png) .png) 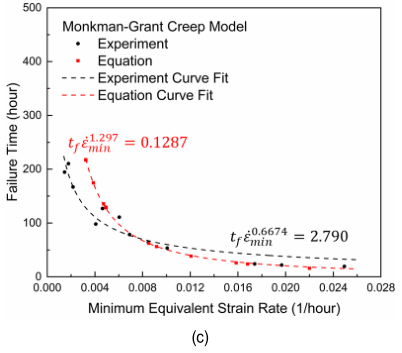
图3 改性9Cr-1Mo钢的蠕变性能评估模型,用于实验和方程式之间的比较:(a)Norton; (b) Larson-Miller; (c) Monkman-Grant
(4)用通过UCT得出的数据构建了Norton、Larson-Miller和Monkman-Grant蠕变特性评估模型,并通过与SPCT构建的模型进行比较,验证了仅通过SPCT得出的数据的有效性。特别是,Norton和Larson-Miller模型在两种测试方法之间显示出相当大的一致性。然而,在Monkman-Grant模型中,两种试验方法之间出现了差异,可能是因为与最小应变率相比,由于SPCT方法将非常薄的试样置于多轴应力状态下,导致断裂时间被低估。
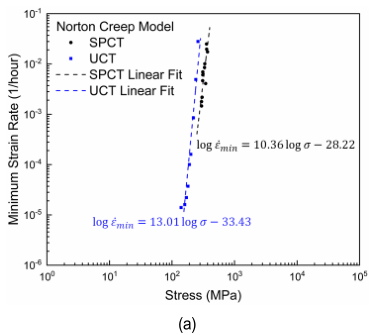 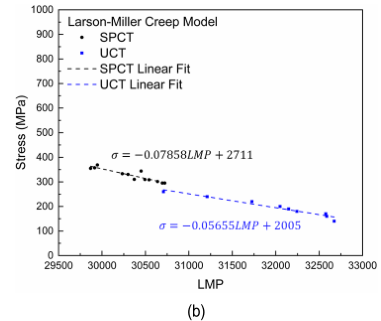 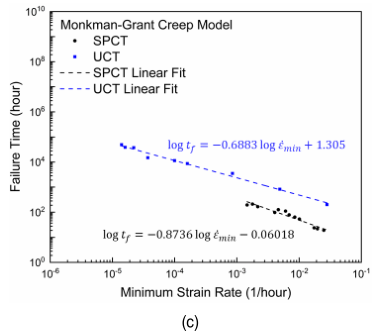
图4 用小冲头和单轴蠕变试验比较的改性9Cr-1Mo钢的蠕变性能评估模型:(a)Norton;(b)Larson-Miller;(c)Monkman-Grant
致谢
本研究由教育部资助的韩国国家研究基金会(NRF)基础科学研究计划(2021R1A6A1A 03039696)支持。本文通讯作者:Kim M K(School of Mechanical Engineering, Sungkyunkwan University, 2066 Seobu-ro, Jangan-gu, Suwon-si, Gyeonggi-do, Korea; SKKU Advanced Institute of Nano Technology (SAINT), Sungkyunkwan University, 2066 Seobu-ro, Jangan-gu, Suwon-si, Gyeonggi-do, Korea)。
本期小编:王家兴(整理)
徐浩波(校对)
王康康(审核)
闵 琳(发布)
|